Explorando los resultados de los modelos de regresión no paramétricos

Explorando los resultados de los modelos de regresión no paramétricos
Kristin MacDonald, Director de Servicios Estadísticos


En su entrada del blog, Enrique Pinzon discutió cómo realizar una regresión cuando no queremos hacer ningún supuesto sobre la forma funcional: usar el comando npregress. Concluyó realizando unas cuantas preguntas y respuestas sobre los resultados usando los comandos magins y marginsplot.

Recientemente, He estado pensando sobre los diferentes tipos de preguntas que podeos responder usando margins después de una regresión no paramétrica, o en realidad después de cualquier tipo de regresión. margins y marginsplot son poderosas herramientas para explorar los resultados de un modelo y extraer distintos tipos de inferencias. En esta publicación, mostraré cómo hacer y responder preguntas muy especificas y cómo explorar toda la superficie de respuesta en función de los resultados de su regresión no paramétrica.

El conjunto de datos que utilizaremos incluye tres covariables: variables continuas x1 y x2 y la variable categórica a con tres niveles. Si desea seguir, puede usar estos datos escribiendo http://www.stata.com/users/kmacdonald/blog/npblog

Primero vamos a ajustar nuestro modelo.

Enrique discute la interpretación de estos resultados en su blog, así que no me enfocaré en esto aquí. Debo señalar, sin embargo, que debido a que mi objetivo es mostrarle cómo usar margins, utilicé solo 10 repeticiones bootstrap (un número ridículamente pequeño) al estimar los errores estándar. En la investigación real, seguramente querrá utilizar más repeticiones tanto con el comando npregress como con los comandos margins que siguen.

El resultado del comando npregress incluye estimaciones de los efectos de x1, x2 y los niveles de a en nuestro resultado, pero estas estimaciones probablemente no sean suficientes para responder algunas de las preguntas importantes que queremos abordar en nuestra investigación.

A continuación, primero te mostraré cómo puedes explorar la respuesta no lineal: el valor esperado de y en diferentes combinaciones de x1, x2 y a. Por ejemplo, suponga que su variable resultado es la respuesta a un medicamento, y desea conocer el valor esperado para una mujer cuyo peso es de 150 libras y cuyo nivel de colesterol es de 220 miligramos por decilitro. ¿Qué tal para un hombre con las mismas características? ¿Cómo cambian estas expectativas en un rango de pesos y niveles de colesterol?

También demostraré cómo responder preguntas sobre promedios poblacionales, contrafactuales, efectos de tratamiento y más. Estos son exactamente los tipos de preguntas que los formuladores de políticas hacen. ¿Cómo, en promedio, una variable afecta a la población en la que están interesados? Por ejemplo, supongamos que su variable resultado es el ingreso de individuos en sus 20 años. ¿Cuál es el valor esperado del ingreso para este grupo, el promedio poblacional? ¿Cuál es el valor esperado si, en lugar de tener su nivel educativo observado, todos fueran graduados de la escuela secundaria? ¿Qué pasaría si todos fueran graduados universitarios? ¿Cuál es la diferencia en estos valores - el efecto de la educación universitaria?

Estos son solo algunos ejemplos de los tipos de preguntas que podría responder. Continuaré con los nombres de variables x1, x2 y a, pero puede imaginar preguntas relevantes para su investigación.


Explorando el área de respuesta.

Empecemos desde el principio. Es posible que deseemos saber el valor esperado del resultado en un punto específico. Para obtener el valor esperado de y cuando a = 1, x1 = 2 y x2 = 5, podemos escribir:

Predecimos que y=12.7 en este punto.

Podemos evaluar en otro punto, digamos, a = 2, x1 = 2, y x2 = 5.

Con a = 2, el valor esperado de y ahora es 14.8.

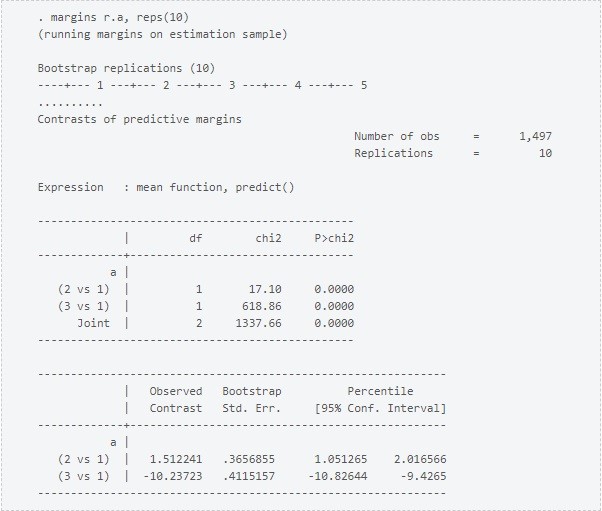
Si nuestro interés está en el efecto de pasar de a = 1 a 2 cuando x1 = 2 y x2 = 5. Esto es solo un contraste: la diferencia en nuestros dos resultados previos. Usando el operador r.  de contraste con margins, podemos realizar una prueba de hipótesis sobre si estos dos valores son los mismos.

El intervalo de confianza para la diferencia no incluye el cero. Usando un nivel de confianza de 5%, encontramos que el valor esperado es significativamente diferente para estos dos puntos de interés.

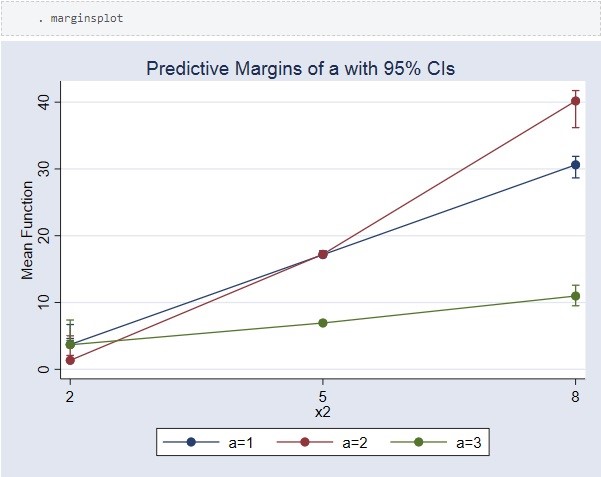
Pero pudiera ser que estemos interesados en más que estos dos puntos, Continuemos manteniendo x2 = 5 y observemos un rango de valores para x1. Y estimamos los valores esperados en los tres niveles de a. En otras palabras, veamos una porción del área de respuesta tridimensional (en x2 = 5) y examinemos la relación entre otras dos variables.

Mejor aún, grafiquemos estos valores.

Encontramos que cuando x2 = 5, el valor esperado de y incrementa al hacerlo x1, y el valor esperado es menor para a = 3 que para a = 1 y a = 2 en todos los niveles de x1.

¿Pero es este patrón el mismo para otros valores de x2?

Tenemos sólo tres covariables. Así que podemos explorar fácilmente toda el área de respuesta. Veamos porciones adicionales en otros valores de x2. Aquí está el comando:

Esto produce una gran cantidad de salida, por lo que no lo mostraré. Pero aquí está el gráfico:

Ahora podemos ver que la superficie de respuesta cambia a medida que x2 cambia. Cuando x2 = 2, el valor esperado de y aumenta ligeramente a medida que x1 aumenta, pero casi no hay diferencia entre los niveles de a. Para x2 = 8, las diferencias entre los niveles de a son más pronunciadas y parecen tener un patrón diferente, aumentando con x1 y luego comenzando a nivelarse.

Anteriormente, escribimos r (1 2).a para probar la diferencia en los valores esperados cuando a = 1 y a = 2. Del mismo modo, podríamos escribir r (1 3).a para comparar a = 1 con a = 3. Podríamos hacer ambas comparaciones simplemente escribiendo r.a. Y podemos hacer esto a través de un rango de valores de x1 y x2. Solo cambiamos a a r.a en nuestro comando previo margins.

La leyenda en la parte superior de la salida nos dice que 1._at corresponde a x1 = 1 y x2 = 2. Los valores en paréntesis, como (2 vs 1), al inicio de cada línea de la tabla nos dicen qué valores de a se comparan en esa línea. Por lo tanto, la primera línea de la tabla proporciona una prueba que compara los valores esperados de y para a = 2 versus a = 1 cuando x1 = 1 y x2 = 2. Es cierto que esto es mucho que mirar, y probablemente sea más fácil de interpretar con un gráfico. Usamos marginsplot para graficar estas diferencias con sus intervalos de confianza. Esta vez, usemos la opción yline(0) para agregar una línea de referencia a 0. Esto nos permite realizar la prueba visualmente al verificar si el intervalo de confianza para la diferencia incluye 0.

En este caso, algunos de los intervalos de confianza son tan estrechos que son difíciles de ver. Si miramos de cerca el punto azul en el extremo izquierdo, vemos que el intervalo de confianza para la diferencia que compara a = 2 versus a = 1 cuando x1 = 1 y x2 = 2 (que corresponde a la primera línea en la salida anterior) incluye el 0. Esto indica que no hay una diferencia significativa en estos valores esperados. Podemos examinar cada uno de los otros puntos e intervalos de confianza de la misma manera. 

Por ejemplo, mirando la línea roja y los puntos en el tercer panel, vemos que el efecto de pasar de a = 1 a a = 3 es negativo y significativamente diferente de 0 para los valores x1 de 2, 3 y 4. Cuando x1 es 1, la estimación puntual del efecto sigue siendo negativa, pero ese efecto no es significativamente diferente de 0 en el nivel del 95%. Pero recordemos que deberíamos aumentar drásticamente la cantidad de repeticiones de arranque para hacer afirmaciones reales sobre los intervalos de confianza.

Hasta ahora, hemos comparado tanto a = 2 con a = 1 como a = 3 con a = 1. Pero no estamos limitados a hacer comparaciones con a = 1. Podríamos comparar 1 con 2 y 2 con 3, lo que a menudo tiene más sentido si los niveles de a tienen un orden natural. Para hacer esto, simplemente reemplazamos r. con ar. en nuestro comando de margins. No mostraré esa salida, pero tienes los datos y puedes probarlos si quieres.


Resultados promediados por población

Hasta ahora, hemos hablado sobre la evaluación de puntos individuales en su superficie de respuesta y cómo realizar pruebas para comparar los valores esperados en esos puntos. Ahora, cambiemos de marcha y hablemos de los resultados promediados por población.

Vamos a necesitar que el conjunto de datos sea representativo de la población. Si eso no es cierto para sus datos, querrá detenerse con los análisis que hicimos anteriormente. Asumiremos que nuestros datos son representativos para que podamos responder una variedad de preguntas basadas en predicciones promedio.

Primero, ¿cuál es el promedio de la población total esperada de esta superficie de respuesta?

Cualquiera que sea el proceso que generó esto, creemos que 15.6 es el valor esperado en la población y [15.3, 16.2] son los intervalos de confianza para él.

¿Difieren los promedios de la población cuando primero establecemos que todos tengan a = 1, luego establecemos que todos tengan a = 2, y finalmente establecemos que todos tengan a = 3? Veamos los promedios esperados para los tres.

Obtuvimos 18.4, 19.9 y 8.2. Parecen no ser iguales. Vamos a probar esta hipótesis.

En la literatura de inferencia causal o de efectos de tratamiento, las medias se considerarían promedios de resultados potenciales, y estas diferencias serían los efectos promedios de tratamiento de un tratamiento multivalor. Aquí el efecto promedio del tratamiento de a = 2 (comparado con a = 1) es 1.5

Vimos en la sección anterior la diferencia en valores esperados para los niveles de valores variados de x2. Estimamos las medias de los resultados potenciales y los efectos del tratamiento de a con diferentes valores de x2. Tenga en cuenta que estos siguen siendo promedios de población porque, a diferencia de la sección anterior, no estamos dando ningún valor especifico a x1. En cambio, las predicciones usan los valores observados de x1 en los datos. 

En lugar de ver la salida, grafiquemos estas medias de resultados potenciales.

El efecto de a se incrementa a medida que incrementa x2. El efecto es mayor cuando x2 = 8.

Ahora, podemos probar las diferencias a cada nivel de x2.

Nuevamente, veamos la gráfica.

La diferencia en medias cuando a = 3 y a = 1, el efecto de tratamiento no es significante cuando x2 = 2. Tampoco el efecto de a = 2 versus a = 1 cuando x2 = 5. Todos los demás efectos son significativamente distintos de 0.


Conclusión

En este blog, hemos explorado el área de respuesta de una función no lineal, hemos estimado una variedad de promedios poblacionales basados en nuestro modelo no paramétrico y hemos realizado diversas pruebas comparando los valores en puntos específicos del área de respuesta y pruebas de hipótesis comparando promedios poblacionales.

Sin embargo, sólo hemos arañado la superficie de los tipos de estimaciones y pruebas que puede obtener usando margins después de npregress. Hay operadores de contrastes adicionales que le permitirán probar las diferencias desde una gran media, diferencias con respecto a los niveles anteriores o posteriores, y más.

Vea [R] contrast para detalles de los operadores de contraste disponibles. También puede usar marginsplot para ver los resultados de los comandos margins desde diferentes ángulos. Por ejemplo, si escribimos marginsplot, bydimension (x1) en lugar de marginsplot, bydimension (x2), vemos nuestra superficie de respuesta no lineal desde una perspectiva diferente. Ver [R] marginsplot para detalles y ejemplos de este comando.

Ya sea que utilice la regresión no paramétrica u otro modelo, margins y  marginsplot son la solución para explorar los resultados, hacer inferencias y comprender las relaciones entre las variables que está estudiando.

Gracias por leer esta entrada. Para cotizaciones de licenciamiento, cursos y libros de Stata, favor de escribirnos a: info@multion.com

Este blog es administrado por MultiON Consulting S.A. de C.V.